Your digital product needs to stay ahead of the competition, which means you need a team who understands modern product development goals and how to achieve them. That’s DocKyard. Book a free consult today to learn more.
Introduction
In this article, we’ll sail the seas of Reinforcement Learning (RL), to tackle route planning for sailboats. There are many variables to be considered, such as the boat’s response to the environment, the sea currents, the wind itself, and the buoys the boat needs to reach, which are called marks.
Over the past year, I’ve been deeply engaged in the study and application of RL, using the “sailboat problem” as my experimental playground. This article serves as the first installment in a series that will explore various RL algorithms and their applications.
The Sailboat Problem
In the sailboat problem, the task is to maneuver a simulated sailboat from a starting point through a designated set of points, which are called marks, in a two-dimensional grid, the racing course. The boat is affected by various environmental factors such as wind speed, direction, and water currents. The objective is not just to get to the endpoint but to do it in the most efficient manner possible, minimizing the time to complete the course. We also wanted to prove that RL could work in Nx, which is why we re-implemented most of the algorithms used in Rein, our RL library written with Nx.
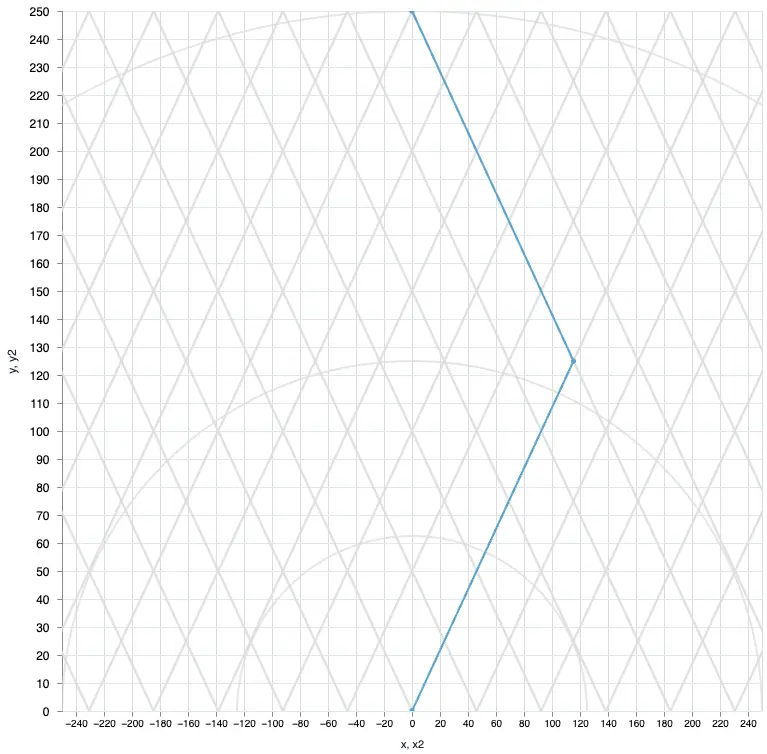
In the first exploratory stages, we tackled the simplest version of this problem, where the wind is fixed in both speed and direction, and only a single mark must be achieved in each iteration. In this situation, there is a theoretical solution that is achieved by following the angle that provides the best Velocity Made Good (VMG) until halfway through the course, and then performing a single tack to reach the target, as the image below shows.
Why Reinforcement Learning?
Reinforcement Learning offers a fitting solution to this problem for several reasons:
- Dynamic Environment: RL algorithms excel in environments that are constantly changing, much like the water current and wind conditions in sailing.
- Optimization: RL aims to find the optimal strategy, or policy, to achieve the highest reward over time. This can be framed in such a way that we can capture what the controller should achieve without assuming how it should do it.
- Adaptability: The same RL framework can adapt to new conditions by learning from the most recent data. This can bring its own set of problems such as catastrophic forgetting, but if applied correctly can generalize in sometimes even unexpected ways.
Techniques Explored
Before we introduce the RL algorithms we explored and will discuss in the future, it’s important to highlight how a well-designed environment makes the most difference. The main difference in performance for our controller between the initial versions with Deep Deterministic Policy Gradients (DDPG) and the current version trained with Proximal Policy Optimization (PPO) isn’t in the algorithms, but the environment and the approach we took in modeling the problem.
Q-Learning
The initial stepping stone in our journey was Q-Learning. This tabular method provided a solid foundation but was limited in handling the complexity and scale of the problem. This is mainly because the Q-table, which we’ll discuss in future iterations, scales with the environment’s complexity and number of variables. It’s also a discrete control algorithm, which limits how we can frame the problem.
DQN (Deep Q-Network)
To overcome the limitations of Q-Learning, we moved on to DQN. It utilizes neural networks to approximate the Q-table, allowing for better generalization and efficiency. It’s still a discrete control algorithm, but the approximation of the Q-table through neural networks allows for the (albeit lossy) representation of much larger spaces for a given memory footprint.
DDPG (Deep Deterministic Policy Gradients)
DDPG was the next natural progression, which helped in dealing with continuous action spaces, crucial for fine-tuned sail adjustments. It’s a similar algorithm to DQN but introduces the idea of actor and critic networks.
SAC (Soft Actor-Critic)
SAC optimized our model further by automatically tuning the temperature parameter, making the algorithm more sample-efficient, as well as providing more insight into more recent techniques. Some of the concepts are taken from DDPG, but it also has similar points to PPO, which was explored next. All the algorithms discussed so far are called off-policy algorithms, in that they learn from all the experience acquired so far, even from past versions of the policy.
PPO (Proximal Policy Optimization)
Lastly, we explored PPO for its stability and robustness, which significantly improved the sailing performance across different environmental conditions. This is where we achieved the best results so far, with faster training and smaller memory footprint. One of the main differences from SAC is that PPO is an on-policy algorithm, which only improves the policy with experiences acquired from the current policy.
So far, PPO is the only algorithm cited that’s not implemented in Rein.
Results
In this first stage, we ended up with SAC as yielding the best results through Rein, while PPO yielded the best results overall.
Soft Actor-Critic
These are results from an in-progress training session. We can see that while the results improve over time, there’s still room for even better-planned paths. We also limited the experiment to just the upwind situation (sailing from the bottom to the top of the graph). This is the more challenging setting, where just tracing a straight line doesn’t reach the target, so it is expected that a policy that manages that can also learn to reach targets in other relative angles to the wind.
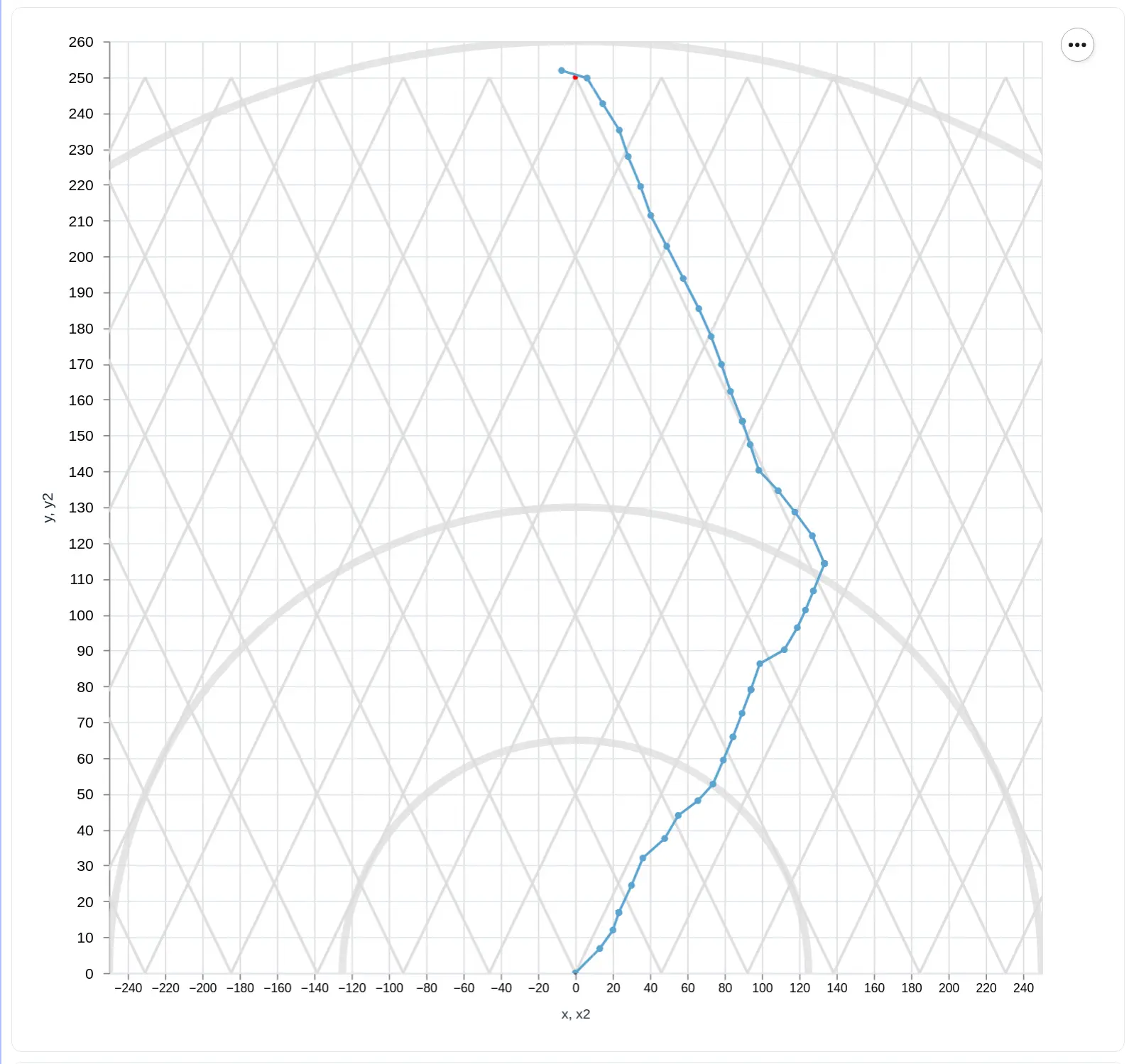
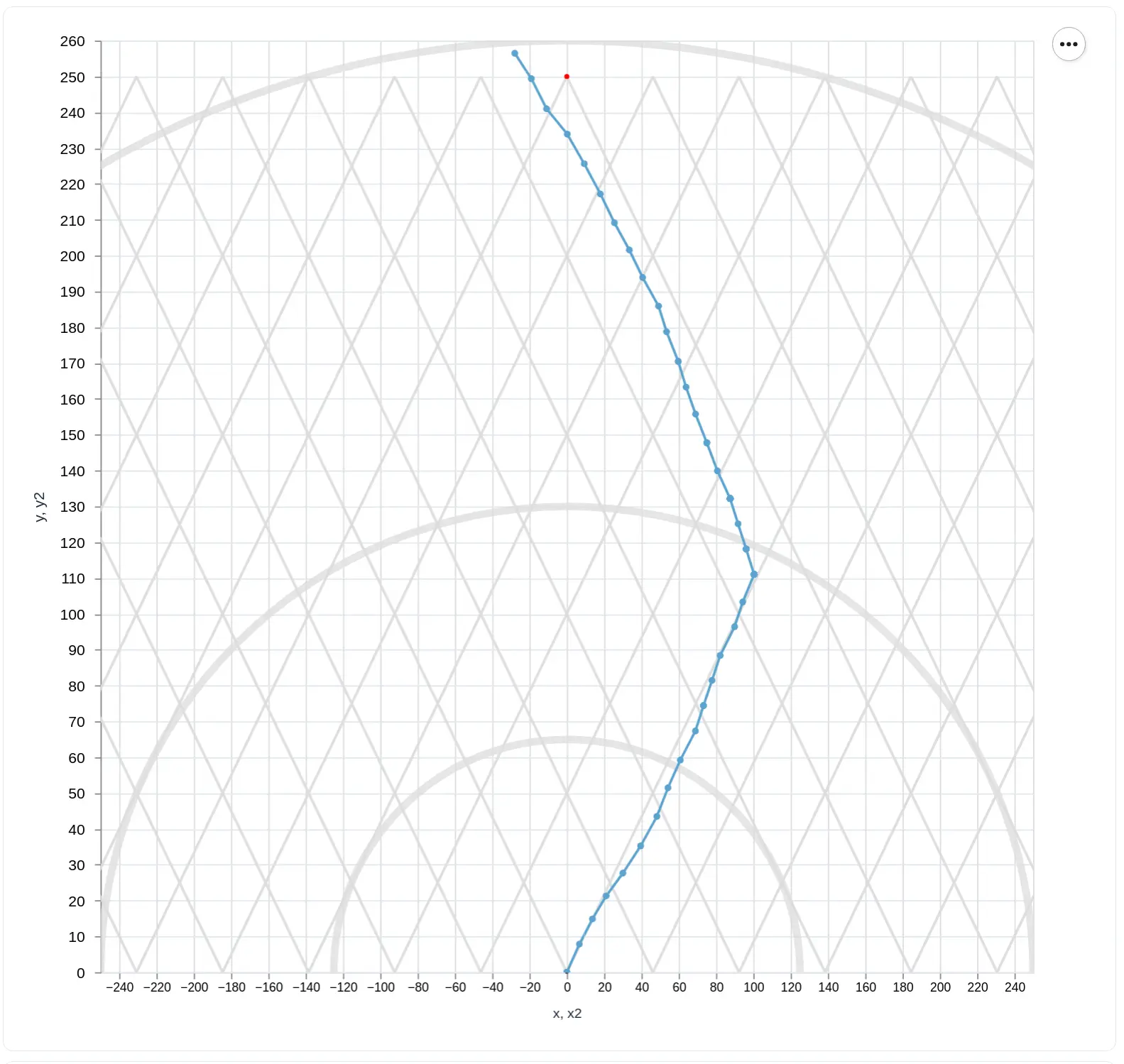
Proximal Policy Optimization
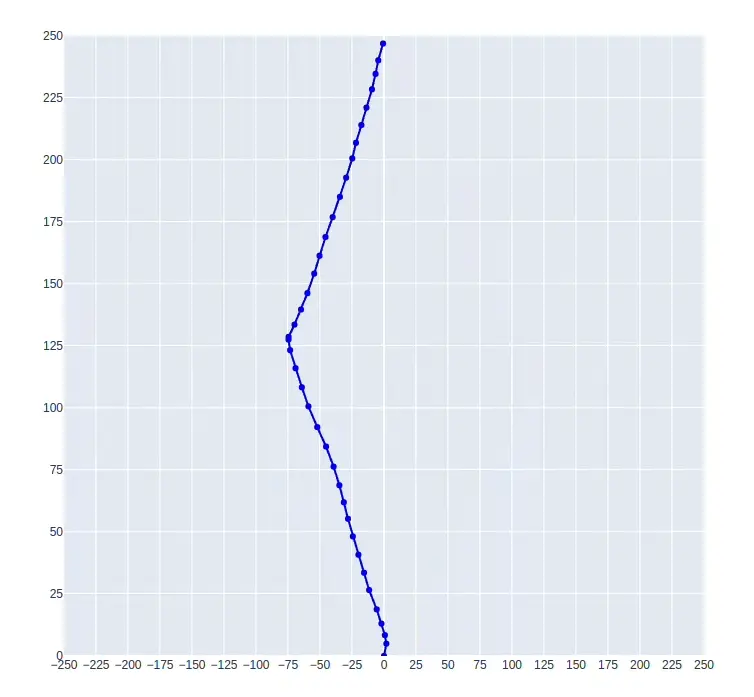
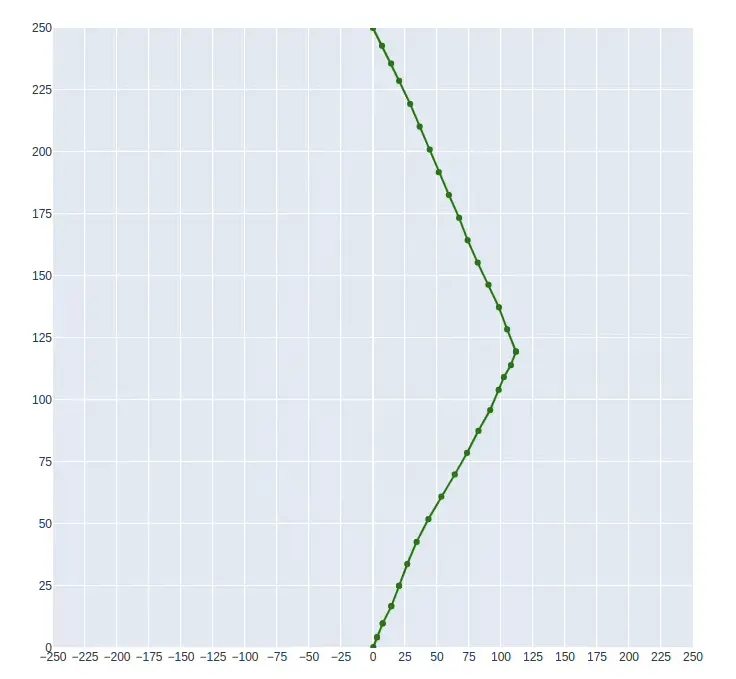
The results for PPO are shown below, also for an in-progress training session. The routes are more consistent throughout different episodes, and the algorithm converged a lot to the solution. One difference from the SAC results is that the agent was able to solve for both the upwind (shown as the blue line in the first image) and downwind (shown as the green line in the second image) situations, as follows:
Conclusion
The sailboat problem provided a rich and challenging sandbox for applying and understanding various reinforcement learning algorithms. From Q-Learning to PPO, each technique offered unique strengths and limitations in tackling the intricate dynamics of sailing. Now that we have solved the proposed environment with PPO, we plan on applying the algorithm to more complicated environments.
As we sail forward, subsequent articles in this series will delve deeper into the applications, similarities, and differences of these algorithms. Stay tuned as we continue navigating the ever-evolving seas of reinforcement learning.